联系我们(内页)
- 电话:15235150078
- 邮箱:1119773998@qq.com
- 网址:www.tyzqxx.com
- 地址:杏花岭区城坊街29号院26号楼万达儿童天地院内(龙潭公园东门)
函数和导数是微积分中重要的概念,它们在数学和科学的各个领域具有广泛的应用。以下将讨论函数与导数的应用。
函数是描述两个变量之间关系的规则。函数可以用来建立模型、预测结果和解决问题。在科学和工程领域中,函数经常用于描述物理过程、经济关系、人口增长等。通过对函数进行分析,可以得到函数的性质、行为和趋势。
导数是函数的变化率或斜率的度量。导数表示了函数在不同点上的变化方式。导数的计算和应用有助于研究函数的最 值、拐点、曲线的凹凸性等特征。以下是几个函数和导数的应用示例:
-
最 优解:导数可以帮助我们找到函数的极 大值和极小值。在经济学中,例如利润最 大化和成本最 小化问题可以通过求解导数为零的情况来获得最 优解。
-
曲线的凹凸性:导数的二阶导数可以帮助我们判断函数曲线的凹凸性。正的二阶导数表示曲线凹向上;负的二阶导数表示曲线凹向下。这可应用于最 佳拟合曲线的选择和图像分析。
-
高阶导数:高阶导数提供了函数更多的信息。例如,速度是位移对时间的导数,加速度是速度对时间的导数。通过高阶导数可以深入了解和描述运动过程。
-
概率密度函数:在统计学中,概率密度函数描述了随机变量的概率分布。通过对概率密度函数求导,可以计算出随机变量的期望值和方差,并进行概率推断。
-
最 速下降法:在优化问题中,最 速下降法利用导数的方向来寻找函数的最 小值。这在数值优化和机器学习等领域有着广泛的应用。
函数和导数的应用涵盖了许多领域,包括物理学、经济学、工程学、统计学等等。它们不仅帮助我们理解和建模实际问题,还推动了科学研究和技术创新的发展。


 周鑫
周鑫 郑渝涵
郑渝涵


 微信号:
微信号: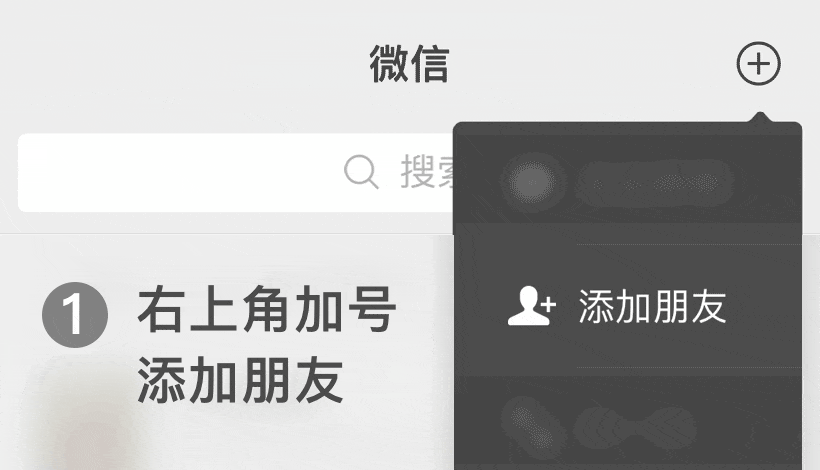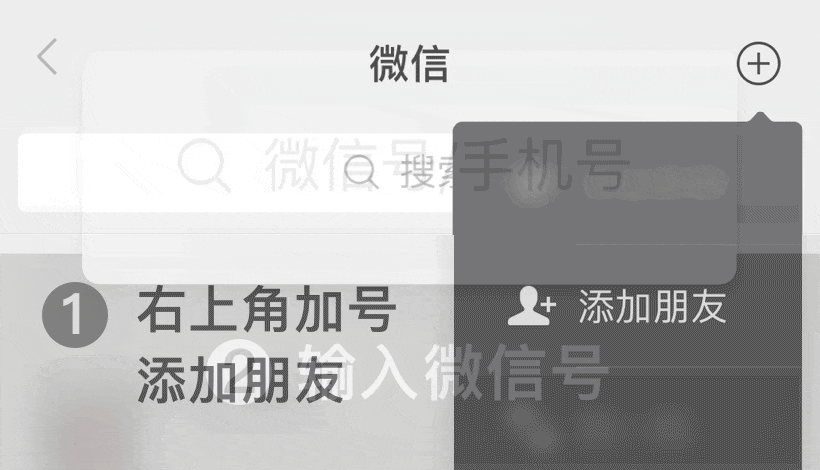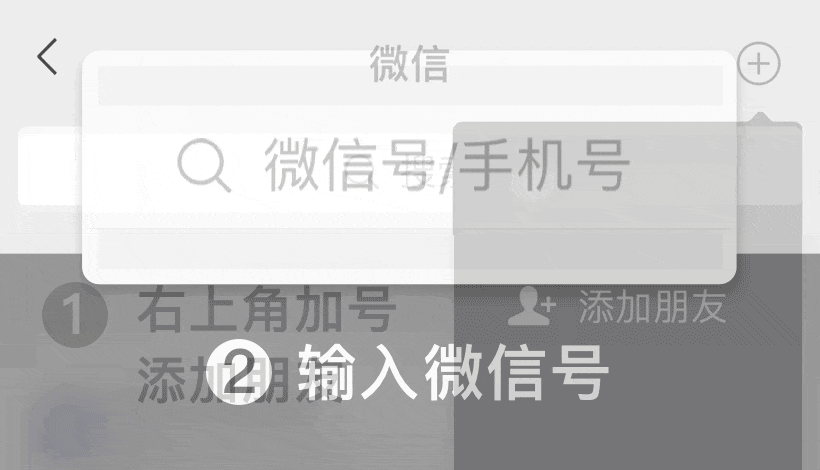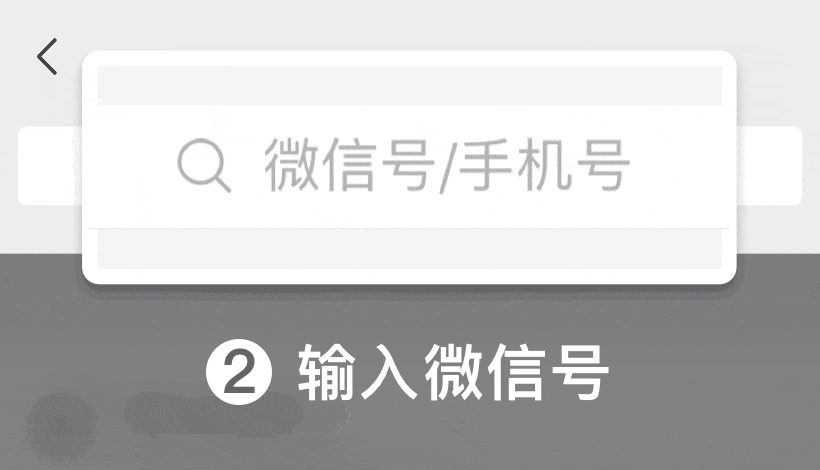
 网站首页
网站首页
 添加微信
添加微信
 电话咨询
电话咨询